Intro to relational databases

This is a terse 5-minute explanation of how relational databases work:


- "An incredibly brief introduction to relational databases"


And these are a couple of YouTube videos explaining why a database is better than a spreadsheet at avoiding inefficient storage and at enforcing the consistency of your data:


- "What is a relational database?"   (5:10 min)
- "Databases and SQL - an introducion"   (9:57 min)

Python-newbie mistakes

Looking back at the code I wrote for the last few posts I realized I made a couple of rookie mistakes. Here they are:

1. I called a variable "range", masking the range() built-in function.

2. I imported norm() and other statistical functions as:

from scipy.stats import norm

This practice is frowned upon, since it might introduce name conflicts. In a longer piece of code, norm() could refer to a normal distribution (in scipy.stats) or to the function used to compute the norm of a vector (in numpy.linalg). As the Zen of Python suggests, "Namespaces are one honking great idea -- let's do more of those!". This is the pythonic way of proceeding:

from scipy import stats

# and then uses stats.norm() for normal distributions

from numpy import linalg

# and linalg.norm() form vector norms

The Kolmogorov-Smirnov test: an example

After introducing the basics about the Kolmogorov-Smirnov test, the plan is now to start from our beloved normal distribution with mean 0 and standard deviation 1, generate n samples of m variates, and use the Kolmogorov-Smirnov test to see for how many samples we can correctly conclude that they have been drawn from the normal distribution (null hypothesis). This is the code I wrote:

import numpy as np
from scipy.stats import norm
from scipy.stats import kstest


mean, sigma, mvariates = 0, 1, 100
np.random.seed(2)


nsamples, rejections = 1000, 0


for i in range(nsamples):
    k, p = kstest(norm.rvs(mean, sigma, size=mvariates), 'norm')
    if p < 0.05:
        rejections = rejections + 1


print 'The null hypothesis is rejected', rejections, '/', nsamples, 'times \
at 5% confidence level.'

For large samples I expected the test to reject the null hypothesis about 5% of the times using a p=0.05 threshold, and this is indeed what happens. But I was surprised to see that even for the smallest samples containing only one variate the test rejects the null hypothesis approximately 5% of the times. It turns out that the sample size is one of the parameters of the kstest() function, and that p-values are computed correctly regardless of the sample size.

Addendum: the code above can be improved

The Kolmogorov-Smirnov test: theory

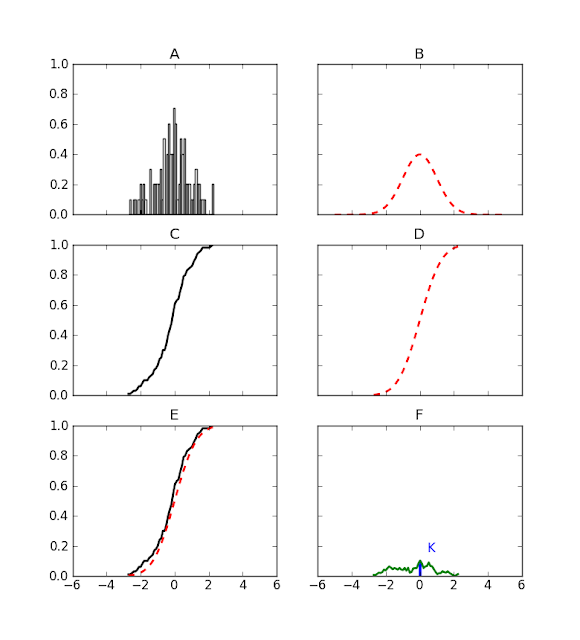
Today's problem is to determine if a sample of N numbers (Fig.A) is compatible with a given probability distribution (Fig.B). Instead of the probability distribution functions we will consider the two cumulative probability distributions (Fig.C and D). The Kolmogorov-Smirnov statistics, K, is the maximum distance from zero of the difference between the two cumulative distribution functions (Fig.E and F). In the ideal limit of infinite data points, the analytic expression for the probability distribtion of K is known and in the next post we will compute the p-value for the initial sample.

Useful Wikipedia links for further reading are:
Kolmogorov-Smirnov test
Donkster's theorem
Brownian bridge


This is the code I used to generate the figures:


import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm
from scipy.stats import cumfreq


mean, sigma, nvariates = 0, 1, 100
np.random.seed(2)
sample = norm.rvs(mean, sigma, size=nvariates)


fig, axs = plt.subplots(nrows=3, ncols=2, sharex=True, sharey=True)


# Fig.A
ax = axs[0, 0]
ax.hist(sample, 50, normed=1, facecolor='white')
ax.set_title('A')


# Fig.B
ax = axs[0, 1]
x = np.arange(-5, 5, 0.001)
ax.plot(x, norm.pdf(x, mean, sigma), 'r--', linewidth=2)
ax.set_title('B')


# Fig.C
ax = axs[1, 0]
partialsums, xmin, xstep, extrapoints = cumfreq(sample, 50)
x = np.arange(xmin, xmin+50*xstep, xstep)
partialfractions = partialsums/nvariates
ax.plot(x, partialfractions, 'k', linewidth=2)
ax.set_title('C')


# Fig.D
ax = axs[1, 1]
ax.plot(x, norm.cdf(x, mean, sigma), 'r--', linewidth=2)
ax.set_title('D')


# Fig.E
ax = axs[2, 0]
ax.plot(x, partialfractions, 'k', linewidth=2)
ax.plot(x, norm.cdf(x, mean, sigma), 'r--', linewidth=2)
ax.set_title('E')


# Fig.F
ax = axs[2, 1]
differences = abs(partialfractions - norm.cdf(x, mean, sigma))
ax.plot(x, differences, color='g', linewidth=2)
xline = xmin+xstep*np.argmax(differences)
yline = np.amax(differences)
ax.vlines(xline, ymin=0, ymax=yline, color='b', linewidth=3)
ax.text(xline+0.5, 1.5*yline, 'K', color='b')
ax.set_title('F')


plt.show()

Addendum: the code above can be improved

Random variables in Python

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm


# generate 1000 instances of a normal random variable
mean, sigma = 0, 1
sample = norm.rvs(mean, sigma, size=1000)


# a 50-bin histogram of the sample
plt.hist(sample, 50, normed=1, facecolor='white')


# the population distribution
range = np.arange(-5, 5, 0.001)
plt.plot(range, norm.pdf(range, mean, sigma), color='red', linewidth=4)


plt.show()

Result:

Addendum: the code above can be improved

How to plot a normal distribution in Python

Python code (slightly adapted from StackOverflow) to plot a normal distribution.

# Plot a normal distribution


import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm


mean = 0
standard_deviation = 1


# Plot between -10 and 10 with .001 steps.
range = np.arange(-10, 10, 0.001)


# Mean = 0, SD = 1.
plt.plot(range, norm.pdf(range, mean, standard_deviation))


plt.show()

Result:

Addendum: the code above can be improved